 プログラムで作図のヘルプ
プログラムで作図のヘルプ プログラムで作図のヘルプ
プログラムで作図のヘルプすぐ作図画面へ
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('gray');
draw_xyaxis();
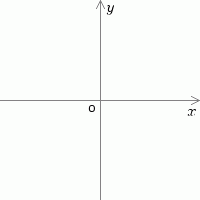
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50); //縮尺と原点の位置を指定する。 //$scale 縮尺 10 は、座標値の1が画面の10ドットに相当することを意味する。 //$org_x_percent 画像の原点の水平位置をパーセントで指定する。50は中央。 //$org_y_percent 画像の原点の垂直位置をパーセントで指定する。50は中央。
set_scale($scale = 10, $org_x_percent = 20, $org_y_percent = 20);
allocate_color('gray');
draw_xyaxis();
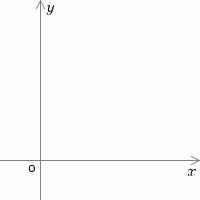
allocate_color($color = 'black'); //線図形の色を指定する。この後に作図する線図形と領域図形に影響する。 //$color 色の名称(red blue など)または、#の後に続く6桁の16進数の色番号 色の名称例(すべての名称が使えるわけではありません)
allocate_bgcolor($color = 'white'); //破線部の色を指定する。この後に作図する線図形に影響する。 //$color 色の名称(red blue など)または、#の後に続く6桁の16進数の色番号 色の名称例(すべての名称が使えるわけではありません)
transparent_bgcolor(); //破線部を透明に指定する。この後に作図する線図形に影響する。 set_thick($thick = 1); //線図形の幅を画像のドット数で指定する。この後に作図する線図形に影響する。 //$thick 線の幅、奇数が好ましい。 set_dashlen($dashlen = 7); //破線の間隔を画像のドット数で指定する。この後に作図する線図形に影響する。 //$dashlen 破線の間隔、5以上が好ましい。 set_arrow_size($arrow_len = 8, $arrow_width = 4); //矢印の長さと幅を画像のドット数で指定する。この後に作図する矢印に影響する。 //$arrow_len 矢印の長さ、8以上が好ましい。 //$arrow_width 矢印の幅、4以上が好ましい。
draw_line($x1, $y1, $x2, $y2); //線分を書く。始点と終点を指定する。 //$x1 始点x座標 //$y1 始点y座標 //$x2 終点x座標 //$y2 終点y座標 draw_horizontal($y); //端から端まで水平線を書く。 //$y y座標 draw_vertical($x); //端から端まで垂直線を書く。 //$x x座標 draw_dash_line($x1, $y1, $x2, $y2); //破線の線分を書く。始点と終点を指定する。 //$x1 始点x座標 //$y1 始点y座標 //$x2 終点x座標 //$y2 終点y座標 draw_rect($x1, $y1, $x2, $y2); //長方形を書く。水平な長方形である。対角点を指定する。 //$x1 対角点1x座標 //$y1 対角点1y座標 //$x2 対角点2x座標 //$y2 対角点3y座標 draw_arrow_head($x1, $y1, $x2, $y2, $pos = 1.0, $count = 1); //矢印の傘を書く。軸の始点と終点を指定する。$pos が 1.0のとき、終点に矢印の傘が付く。 //$x1 始点x座標 //$y1 始点y座標 //$x2 終点x座標 //$y2 終点y座標 //$pos 傘の位置 0:始点 から 1:終点 //$count 傘の数(1, 2, 3, ...) draw_xaxis($x_is_low_pos = true, $sx = false, $ex = false); //X軸を書く、原点を通ります。 //$x_is_low_pos 記号xを下に書くか、上に書くか //$sx X軸の開始座標、画面左端にするときは false //$ex X軸の終了座標、画面右端にするときは false draw_yaxis($y_is_right_pos = true, $sy = false, $ey = false); //Y軸を書く、原点を通ります。 //$y_is_right_pos 記号yを右に書くか、左に書くか //$sy Y軸の開始座標、画面下端にするときは false //$ey Y軸の終了座標、画面上端にするときは false draw_xyaxis(); //X軸Y軸を書く、原点を通ります。 draw_circle($cx, $cy, $r); //円を書く //$cx 中心点x座標 //$cy 中心点y座標 //$r 半径 (正の数) draw_arc_deg($cx, $cy, $r, $sa, $ea); //円弧を書く //$cx 中心点x座標 //$cy 中心点y座標 //$r 半径 (正の数) //$sa 開始角(度単位) //$ea 終了角(度単位) draw_arc($cx, $cy, $r, $sa, $ea); //円弧を書く //$cx 中心点x座標 //$cy 中心点y座標 //$r 半径 (正の数) //$sa 開始角(ラジアン単位) //$ea 終了角(ラジアン単位) draw_dash_arc($cx, $cy, $r, $sa, $ea); //破線の円弧を書く //$cx 中心点x座標 //$cy 中心点y座標 //$r 半径 (正の数) //$sa 開始角(ラジアン単位) //$ea 終了角(ラジアン単位)
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('black');
draw_line(-7, -7, 7, 7);
allocate_color('red');
draw_horizontal(0);
allocate_color('blue');
draw_vertical(0);
allocate_color('green');
set_thick(3);
draw_dash_line(-7, 7, 7, -7);
allocate_color('purple');
set_thick(1);
draw_rect(-8, -8, 8, 8);
allocate_color('black');
draw_circle(-8, -8, 2);
set_thick($thick = 3);
allocate_color('red');
draw_circle(8, 8, 2);
set_thick(1);
allocate_color('blue');
draw_arc_deg(0, 0, 5, 45, 135);
set_thick($thick = 3);
allocate_color('green');
draw_arc(0, 0, 5, deg2rad(225), deg2rad(315));
set_thick(1);
allocate_color('purple');
draw_dash_arc(0, 0, 6, deg2rad(45), deg2rad(135));
set_thick($thick = 3);
allocate_color('black');
draw_dash_arc(0, 0, 6, deg2rad(225), deg2rad(315));
set_dashlen($dashlen = 10);
transparent_bgcolor();
set_thick(1);
allocate_color('purple');
draw_dash_line(-6, 1, 6, 1);
set_dashlen($dashlen = 5);
allocate_color('black');
draw_dash_line(-6, -1, 6, -1);
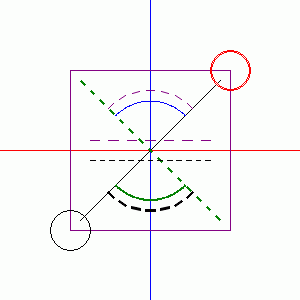
fill_rect($x1, $y1, $x2, $y2); //長方形を塗りつぶす。水平な長方形である。対角点を指定する。 //$x1 対角点1x座標 //$y1 対角点1y座標 //$x2 対角点2x座標 //$y2 対角点3y座標 fill_circle($cx, $cy, $r); //円を塗りつぶす。 //$cx 中心点x座標 //$cy 中心点y座標 //$r 半径 (正の数) fill_arc_deg($cx, $cy, $r, $sa, $ea); //円弧を塗りつぶす。 //$cx 中心点x座標 //$cy 中心点y座標 //$r 半径 (正の数) //$sa 開始角(度単位) //$ea 終了角(度単位) fill_triangle($ax, $ay, $bx, $by, $cx, $cy); //三角形を塗りつぶす。 fill_quadrangle($ax, $ay, $bx, $by, $cx, $cy, $dx, $dy); //四角形を塗りつぶす。 fill_polygon($points_xy); //多角形を塗りつぶす。 //$points_xy 配列 array() で、頂点のx座標y座標を交互に指定する。 fill_toborder($x, $y, $border_color_x, $border_color_y); //ある点から塗りつぶす。境界の点と同じ色にあたると塗りつぶしは止まる。 //$x ある点x座標 //$y ある点y座標 //$border_color_x 境界の点x座標 //$border_color_y 境界の点y座標
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('black');
fill_rect($x1 = -9, $y1 = -9, $x2 = -8, $y2 = -8);
allocate_color('red');
fill_rect($x1 = -7, $y1 = -7, $x2 = -5, $y2 = -5);
allocate_color('blue');
fill_arc_deg($cx = -8, $cy = 8, $r = 3, $sa = 90, $ea = 180);
allocate_color('green');
fill_arc_deg($cx = -7.5, $cy = 7.5, $r = 3, $sa = 250, $ea = 380);
allocate_color('purple');
fill_circle($cx = -3, $cy = 3, $r = 2);
allocate_color('yellow');
fill_triangle($ax = 1, $ay = 1, $bx = 4, $by = 1, $cx = 1, $cy = 6);
allocate_color('red');
fill_quadrangle($ax = 4, $ay = 4, $bx = 8, $by = 4,
$cx = 9, $cy = 7, $dx = 5, $dy = 7);
allocate_color('blue');
$cx = 3;
$cy = -3;
$r = 3;
$pts = array();
for($i = 0; $i <= 8; ++$i){
if(fmod($i, 2) == 0){
$tr = $r;
}else{
$tr = $r * 0.3;
}
$pts[] = $cx + $tr * cos(M_PI * $i / 4);
$pts[] = $cy + $tr * sin(M_PI * $i / 4);
}
fill_polygon($pts);
allocate_color('black');
draw_circle($c1x = 5, $c1y = -9, $r1 = 3);
draw_circle($c2x = 8, $c2y = -9, $r2 = 3);
allocate_color('green');
fill_toborder($x = ($c1x + $c2x) / 2, $y = ($c1y + $c2y) / 2,
$border_color_x = $c1x + $r1, $border_color_y = $c1y);
allocate_color('yellow');
fill_toborder($x = $c1x - $r1 / 2, $y = $c1y,
$border_color_x = $c1x - $r1, $border_color_y = $c1y);
allocate_color("#CCFF33");
fill_toborder($x = $c2x + $r2 / 2, $y = $c2y,
$border_color_x = $c2x + $r2, $border_color_y = $c2y);
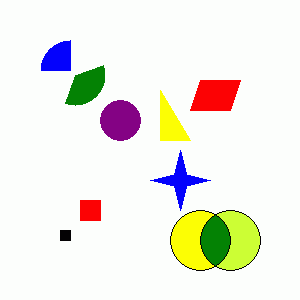
allocate_text_color($color = 'black'); //文字の色を指定する。この後に作図する文字と数式に影響する。 //$color 色の名称(red blue など)または、#の後に続く6桁の16進数の色番号 色の名称例(すべての名称が使えるわけではありません)
allocate_text_bgcolor($color = 'white'); //文字の背景色を指定する。この後に作図する文字と数式に影響する。 //$color 色の名称(red blue など)または、#の後に続く6桁の16進数の色番号 色の名称例(すべての名称が使えるわけではありません)
transparent_text_bgcolor(); //文字の背景を透明に指定する。この後に作図する文字と数式に影響する。 set_text_size($text_size); //文字の大きさを指定する。この後に作図する文字に影響する。 //$text_size 画面のドット数で指定する。 set_text_margin($text_margin); //文字を囲むマージンを指定する。この後に作図する文字と数式に影響する。 //$text_margin 画面のドット数で指定する。マージンは、上下左右にこの幅で付く。 set_mark_size($mark_size); //マークの大きさを指定する。この後に作図するマークに影響する。 //$text_margin 画面のドット数で指定する。
draw_text($utf_8_text = 'ABC', $x = 3, $y = 2, $o_pos = O_POS_LOW_LEFT, $italic = false); //文字を描く //$utf_8_text 文字列、日本語も可能 //$x 文字の基準点の x 座標 //$y 文字の基準点の y 座標 //$o_pos 文字の配置方法、文字列全体に対して、基準点がどこにあるかを示す //$italic イタリックにするときは、trueを指定する // (日本語があるとイタリックにはできない、ゴシックか明朝になる) // (イタリックでは、英数字だけを使うこと記号があると形がくずれる) // 次のフォント名を指定することもできる。 // 'serif'(), 'italic', 'ipagp'(日本語ゴシック) , 'ipamp'(日本語明朝) // O_POS_LOW_LEFT 左下 // O_POS_LOW_RIGHT 右下 // O_POS_UP_RIGHT 右上 // O_POS_UP_LEFT 左下 // O_POS_LOW_CENTER 中央下 // O_POS_MIDDLE_RIGHT 右中段 // O_POS_UP_CENTER 中央上 // O_POS_MIDDLE_LEFT 左中段 // O_POS_MIDDLE_CENTER 中央中段 $o_pos = get_o_pos_by_ang($ang); //角度から文字がよく見えるの配置方法を返す //$ang 角度(ラジアン) draw_formula($formula_text = 'y=ax^2+bx+c', $size = 12, $px = 0, $py = 0, $o_pos = O_POS_LOW_LEFT); //数式を描く //$formula_text 数式の文字列 // (数式の指定はこちらを参考。) // (ただし、<m> と </m> で囲む必要はない) //$size 数式の文字の大きさ、画面のドット数で指定 //$x 数式の基準点の x 座標 //$y 数式の基準点の y 座標 //$o_pos 数式の配置方法、数式に対して、基準点がどこにあるかを示す draw_arc_mark(&$tx, &$ty, $ax, $ay, $bx, $by, $text = '2R', $italic = true, $arc_end_type = ARC_TYPE_DASH, $width_rate = 1, $text_hole_rate = 1.7); //円弧による辺の説明線を描く //&$tx 説明文字の位置の x 座標 (この座標は、関数から呼び出し側へ戻される) //&$ty 説明文字の位置の y 座標 (この座標は、関数から呼び出し側へ戻される) //$ax 円弧の始点の x 座標 //$ay 円弧の始点の y 座標 //$bx 円弧の終点の x 座標 //$by 円弧の終点の y 座標 // (円弧の中心は、始点から終点に向かって左となる) //$text 説明文字 //$italic 説明文字の書体(draw_textを参考) //$arc_end_type 円弧の種類と始点・終点の矢印の有無 // ARC_TYPE_NONE 円弧を描かない // ARC_TYPE_SOLID 実線の円弧 // ARC_TYPE_DASH 破線の円弧 // BEG_TYPE_ARROW 始点の矢印有(ARC_TYPE_SOLID等に加算する) // END_TYPE_ARROW 終点の矢印有(ARC_TYPE_SOLID等に加算する) //$width_rate 文字の大きさに対して円弧のふくらみの比率 //$text_hole_rate 文字を書くため、円弧の中央部を切り取る穴の比率(文字の大きさに対して) draw_corner_mark($cx = 0, $cy = 0, $ax = 1, $ay = 0, $bx = 0, $by = 1, $type = 1, $text = 'A', $italic = true, $text_ops = 'A', $italic_ops = false, $r = 10); //角のマークを書く //$cx 角の頂点の x 座標 //$cy 角の頂点の y 座標 //$ax 角の開始辺の上の一点の x 座標 //$ay 角の開始辺の上の一点の y 座標 //$bx 角の終了辺の上の一点の x 座標 //$by 角の終了辺の上の一点の y 座標 //$type 角のマークの種類 // 0:CMARK_NONE:書かない // 1:CMARK_1_ARC:小円弧 // 2:CMARK_2_ARC:二重の小円弧 // 3:CMARK_D_ARC:小円弧にダッシュ // 4:CMARK_1_PIE:小円弧・塗り有 // 5:CMARK_2_PIE:二重の小円弧・塗り有 // 6:CMARK_D_PIE:小円弧にダッシュ・塗り有) // CMARK_SQUARE:四角 // CMARK_CROSS:× // CMARK_CIRCLE:○ // CMARK_DOT:● //$text 説明文字(角の内側) //$italic 説明文字の書体(draw_textを参考) //$text_ops 説明文字(角の外側) //$italic_ops 説明文字の書体(draw_textを参考) //$r 角のマークの大きさ(画面のドット数) draw_marked_triangle($ax = 1, $ay = 0, $bx = 1, $by = 1, $cx = 0, $cy = 0, $type_a = 1, $type_b = 2, $type_c = 3, $text_a = 'A', $text_b = 'B', $text_c = 'C', $text_ops_a = 'A', $text_ops_b = 'B', $text_ops_c = 'C', $italic = true, $italic_ops = false, $r = 10); //角のマークつきの三角形を書く //$ax 三角形の頂点1の x 座標 //$ay 三角形の頂点1の y 座標 //$bx 三角形の頂点2の x 座標 //$by 三角形の頂点2の y 座標 //$cx 三角形の頂点3の x 座標 //$cy 三角形の頂点3の y 座標 //$type_a 三角形の頂点1の角のマークの種類 (draw_corner_mark を参考) //$type_b 三角形の頂点2の角のマークの種類 (draw_corner_mark を参考) //$type_c 三角形の頂点3の角のマークの種類 (draw_corner_mark を参考) //$text_a 三角形の頂点1の説明文字(角の内側) //$text_b 三角形の頂点2の説明文字(角の内側) //$text_c 三角形の頂点3の説明文字(角の内側) //$text_ops_a 三角形の頂点1の説明文字(角の外側) //$text_ops_b 三角形の頂点2の説明文字(角の外側) //$text_ops_c 三角形の頂点3の説明文字(角の外側) //$italic 説明文字の書体(draw_textを参考) //$italic_ops 説明文字の書体(draw_textを参考) //$r 角のマークの大きさ(画面のドット数) draw_mark($px = 0, $py = 0, $angle = 0, $type = MARK_1_LINE); //マークを書く //$px マークの中心 x 座標 //$py マークの中心 y 座標 //$angle マークの角度(ラジアン) //$type マークの種類 // MARK_1_LINE : 縦線 // MARK_2_LINE : 二本線 // MARK_3_LINE : 三本線 // MARK_SQUARE : 四角形 // MARK_CROSS : × // MARK_CIRCLE : ○ // MARK_DOT : ● //マークの大きさは、set_mark_size draw_mark_on_line($x1, $y1, $x2, $y2, $type = MARK_1_LINE, $pos = 0.5) //直線上にマークを書く //$x1 直線の始点 x 座標 //$y1 直線の始点 y 座標 //$x2 直線の終点 x 座標 //$y2 直線の終点 y 座標 //$type マークの種類(draw_mark を参考) //マークの大きさは、set_mark_size //$pos 直線上のマーク位置の割合 0 から 1 draw_mark_on_circle($cx, $cy, $r, $angle, $type = MARK_1_LINE) //円上にマークを書く //$cx 円の中心 x 座標 //$cy 円の中心 y 座標 //$r 円の半径 //$angle 円上のマーク位置の角度(ラジアン) //$type マークの種類(draw_mark を参考) //マークの大きさは、set_mark_size
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_text_color('black');
allocate_text_bgcolor('#CCFF99');
draw_text($utf_8_text = 'LOW&LEFT', $x = -0, $y = 7, $o_pos = O_POS_LOW_LEFT, $italic = false);
draw_text($utf_8_text = 'LOW&RIGHT', $x = -1, $y = 7, $o_pos = O_POS_LOW_RIGHT, $font = 'italic');
draw_text($utf_8_text = 'UP&LEFT', $x = 0, $y = 6, $o_pos = O_POS_UP_LEFT, $italic = true);
draw_text($utf_8_text = 'UP&RIGHT', $x = -1, $y = 6, $o_pos = O_POS_UP_RIGHT, $font = 'serif');
allocate_text_color('green');
transparent_text_bgcolor();
draw_text($utf_8_text = 'lowcenter', $x = 0, $y = 0, $o_pos = O_POS_LOW_CENTER, $italic = true);
draw_text($utf_8_text = 'upcenter', $x = 0, $y = -4, $o_pos = O_POS_UP_CENTER, $italic = true);
draw_text($utf_8_text = 'middleright', $x = -5, $y = -2, $o_pos = O_POS_MIDDLE_RIGHT, $italic = true);
draw_text($utf_8_text = 'middleleft', $x = 5, $y = -2, $o_pos = O_POS_MIDDLE_LEFT, $italic = true);
draw_text($utf_8_text = 'middlecenter', $x = 0, $y = -2, $o_pos = O_POS_MIDDLE_CENTER, $italic = true);
allocate_text_color('blue');
allocate_text_bgcolor('#AFEEEE');
set_text_size(30);
draw_text($utf_8_text = '日本語', $x = 1, $y = 10, $o_pos = O_POS_LOW_LEFT, $font = 'ipamp');
allocate_text_color('purple');
allocate_text_bgcolor('#FF8C00');
set_text_size(30);
draw_text($utf_8_text = '日本語', $x = -14, $y = 10, $o_pos = O_POS_LOW_LEFT, $font = 'ipagp');
allocate_text_color('black');
allocate_text_bgcolor('white');
draw_formula($formula_text = 'x={-b pm sqrt{b^2-4ac}}/{2a}', $size = 12, $px = 0, $py = -7, $o_pos = O_POS_MIDDLE_CENTER);

set_x_def_range($xds = -10, $xde = 10, $equal_xds = true, $equal_xde = true); //y=f(x)型の関数の定義域(xの範囲)を指定する。 //$xds 定義域の小さいほう //$xde 定義域の大きいほう //$equal_xds $xdsを含めるか(true)、含めないか(false) //$equal_xde $xdeを含めるか(true)、含めないか(false) df1_ax_b($a, $b); //一次関数 y = ax + b のグラフを書く // (set_x_def_range()の範囲となる) //$a 係数(傾き) //$b 係数(y軸の切片) df1_x_y($x, $y); //x軸の切片とy軸の切片を指定して 一次関数 のグラフを書く // (set_x_def_range()の範囲となる) //$x x軸の切片 //$y y軸の切片 df1_2p($x1, $y1, $x2, $y2); //二点を通る 一次関数 のグラフを書く // (set_x_def_range()の範囲となる) df2_ax2_bx_c($a = 1, $b = 0, $c = 0); //ニ次関数 y = ax^2 + bx + c のグラフを書く // (set_x_def_range()の範囲となる) df2_ax_p2_q($a = 1, $p = 2, $q = -1); //ニ次関数 y = a(x - p)^2 + q のグラフを書く // (set_x_def_range()の範囲となる) df2_a_x_al_x_be($a = 1, $alpha = -1, $beta = 1); //ニ次関数 y = a(x - alpha)(x - beta) のグラフを書く // (set_x_def_range()の範囲となる) df_y_fx($y_fx_name = 'y_fx'); //ユーザ定義関数のグラフを書く // (ユーザ定義の関数は、 php の 関数(function)として作成してください。) // (関数の定義域は、 set_x_def_range()の範囲となります) //$y_fx_name ユーザ定義関数の名前 // ユーザ定義関数は、引数$xを一つとり $yを 戻す関数であること。 df_xt_yt($xt_name = 'xt', $yt_name = 'yt', $ts = 0, $te = 1, $div = 32); //ユーザ定義曲線(媒介変数$t)のグラフを書く //$xt_name ユーザ定義曲線 x = f(t) の関数の名前 //$yt_name ユーザ定義曲線 y = g(t) の関数の名前 // (ユーザ定義曲線の関数は、 php の 関数(function)として作成してください。) //$ts 媒介変数の開始値 //$te 媒介変数の終了値 //$div 曲線を媒介変数で等分割して曲線近似するときの分割数
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('gray');
draw_xyaxis();
allocate_color('black');
//set_x_def_range($xds = -10, $xde = 10);
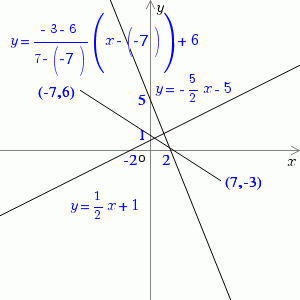
df1_ax_b($a = 0.5, $b = 1);
allocate_text_color('blue');
draw_formula($formula_text = 'y={1/2}x+1', $size = 12, $px =-8, $py = -4, $o_pos = O_POS_UP_LEFT);
draw_text("1", $x = -0.8, $y = 1, $o_pos = O_POS_LOW_RIGHT, $italic = false);
draw_text("-2", $x = -2, $y = -0.5, $o_pos = O_POS_UP_CENTER, $italic = false);
df1_x_y($x = 2, $y = 5);
draw_formula($formula_text = 'y = -{5/2} x - 5', $size = 12, $px = 0.5, $py = 6, $o_pos = O_POS_MIDDLE_LEFT);
draw_text("5", $x = -0.4, $y = 5, $o_pos = O_POS_MIDDLE_RIGHT, $italic = false);
draw_text("2", $x = 2, $y = -0.5, $o_pos = O_POS_UP_RIGHT, $italic = false);
set_x_def_range($xds = -7, $xde = 7);
df1_2p($x1 = -7, $y1 = 6, $x2 = 7, $y2 = -3);
draw_formula($formula_text = 'y = {{-3 - 6}/{7-(-7)}} (x - (-7)) + 6', $size = 12, $px = -14, $py = 14, $o_pos = O_POS_UP_LEFT);
draw_text("(-7,6)", $x = -7.5, $y = 6, $o_pos = O_POS_MIDDLE_RIGHT);
draw_text("(7,-3)", $x = 7.5, $y = -3, $o_pos = O_POS_MIDDLE_LEFT);
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('gray');
draw_xyaxis();
allocate_color('black');
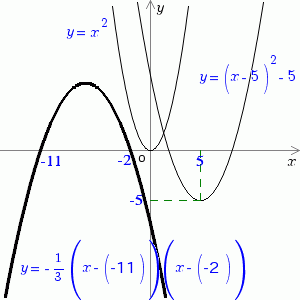
df2_ax2_bx_c($a = 1, $b = 0, $c = 0);
allocate_text_color('blue');
draw_formula("y=x^2", $size = 12, $px = -sqrt(12) - 0.5, $py = 12, $o_pos = O_POS_MIDDLE_RIGHT);
df2_ax_p2_q($a = 1/2, $p = 5, $q = -5);
allocate_color('green');
draw_dash_line(5, 0, 5, -5);
draw_dash_line(0, -5, 5, -5);
allocate_color('black');
draw_text('5', $x = 5, $y = -0.5, $o_pos = O_POS_UP_CENTER);
draw_text('-5', $x = -0.8, $y = -5, $o_pos = O_POS_MIDDLE_RIGHT);
draw_formula("y=(x-5)^2-5", $size = 12, $px = 10, $py = (10-5)*(10-5)/2-5, $o_pos = O_POS_MIDDLE_CENTER);
set_thick($thick = 3);
df2_a_x_al_x_be($a = -1/3, $alpha = -11, $beta = -2);
draw_text('-11', $x = -11, $y = -0.5, $o_pos = O_POS_UP_LEFT);
draw_text('-2', $x = -2, $y = -0.5, $o_pos = O_POS_UP_RIGHT);
draw_formula("y=-{1/3}(x-(-11))(x-(-2))", $size = 12, $px = -13, $py = -8.7, $o_pos = O_POS_UP_LEFT);
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('gray');
draw_xyaxis();
allocate_color('black');
set_x_def_range($xds = 0, $xde = 15);
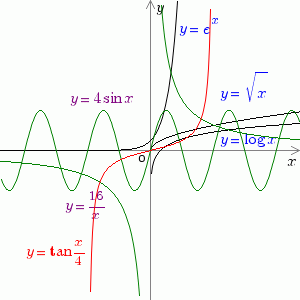
df_y_fx(sqrt);
allocate_text_color('blue');
draw_formula("y=sqrt{x}", $size = 12, $px = 7, $py = sqrt(7) + 2, $o_pos = O_POS_LOW_LEFT);
set_x_def_range($xds = -15, $xde = 15);
df_y_fx(exp);
draw_formula("y=e^x", $size = 12, $px = 2.4+0.5, $py = exp(2.4), $o_pos = O_POS_LOW_LEFT);
set_x_def_range($xds = 0, $xde = 15, $equal_xds = false, $equal_xde = true);
df_y_fx(log);
draw_formula("y=log x", $size = 12, $px = 7, $py = log(7), $o_pos = O_POS_UP_LEFT);
allocate_color('green');
set_x_def_range($xds = -15, $xde = 0, $equal_xds = true, $equal_xde = false);
function x_inv($x){return 16/$x;}
df_y_fx(x_inv);
set_x_def_range($xds = 0, $xde = 15, $equal_xds = false, $equal_xde = true);
df_y_fx(x_inv);
allocate_text_color('purple');
draw_formula("y=16/x", $size = 12, $px = -4, $py = -4, $o_pos = O_POS_UP_RIGHT);
set_x_def_range($xds = -15, $xde = 15, $equal_xds = false, $equal_xde = false);
function sin4($x){return 4*sin($x);}
df_y_fx(sin4);
draw_formula("y=4sin x", $size = 12, $px = M_PI * (-3/2), $py = 4, $o_pos = O_POS_LOW_CENTER);
set_x_def_range($xds = -2 * M_PI, $xde = 2 * M_PI, $equal_xds = false, $equal_xde = false);
function tan4($x){return tan($x/4);}
allocate_color('red');
df_y_fx(tan4);
allocate_text_color('red');
draw_formula("y=sin x/4", $size = 12, $px = -6, $py = -12, $o_pos = O_POS_LOW_RIGHT);
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
allocate_color('gray');
draw_xyaxis();
allocate_color('black');
function ellipse_x($t)
{$cx = 7; $cy = 4; $a = 5; $b = 2.5; return $a * cos($t) + $cx;}
function ellipse_y($t)
{$cx = 7; $cy = 4; $a = 5; $b = 2.5; return $b * sin($t) + $cy;}
df_xt_yt('ellipse_x', 'ellipse_y', 0, 2 * M_PI, $div = 32);
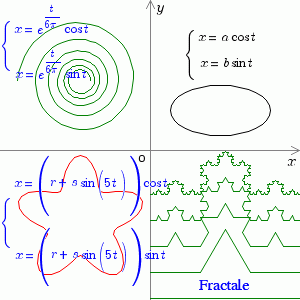
draw_formula("{lbrace}matrix{2}{1}{{x=a cos t}{x=b sin t}}", $size = 12, $px = 7, $py = 10, $o_pos = O_POS_MIDDLE_CENTER);
allocate_color('red');
function star_x($t)
{$cx = -7; $cy = -7; $r = 5; $s = 1.5;
return ($r + $s * sin($t * 5)) * cos($t) + $cx;}
function star_y($t)
{$cx = -7; $cy = -7; $r = 5; $s = 1.5;
return ($r + $s * sin($t * 5)) * sin($t) + $cy;}
df_xt_yt('star_x', 'star_y', 0, 2 * M_PI, $div = 64);
allocate_text_color('blue');
draw_formula("{lbrace}matrix{2}{1}{{x=(r + s sin(5t)) cos t}{x=(r + s sin(5t)) sin t}}", $size = 12, $px = -15, $py = 0, $o_pos = O_POS_UP_LEFT);
allocate_color('green');
function roll_x($t)
{$cx = -7; $cy = 7; $r = 1;
return ($r * exp($t / (3 * 2 * M_PI))) * cos($t) + $cx;}
function roll_y($t)
{$cx = -7; $cy = 7; $r = 1;
return ($r * exp($t / (3 * 2 * M_PI))) * sin($t) + $cy;}
df_xt_yt('roll_x', 'roll_y', 0, 11 * M_PI, $div = 256);
draw_formula("{lbrace}matrix{2}{1}{{x=e^{t/{6 pi}} cos t}{x=e^{t/{6 pi}} sin t}}", $size = 12, $px = -15, $py = 15, $o_pos = O_POS_UP_LEFT);
function fractale($x1, $y1, $x2, $y2, $nest)
{
if($nest > 0){
--$nest;
$px = ($x1 * 2 + $x2) / 3;
$py = ($y1 * 2 + $y2) / 3;
$qx = ($x1 + $x2 * 2) / 3;
$qy = ($y1 + $y2 * 2) / 3;
$u = $x2 - $x1;
$v = $y2 - $y1;
$len = (unit_vector($u, $v) / 3) * sqrt(3) / 2;
rot90_vec($u, $v, $u90, $v90);
$rx = ($x1 + $x2) / 2 + $len * $u90;
$ry = ($y1 + $y2) / 2 + $len * $v90;
fractale($x1, $y1, $px, $py, $nest);
fractale($px, $py, $rx, $ry, $nest);
fractale($rx, $ry, $qx, $qy, $nest);
fractale($qx, $qy, $x2, $y2, $nest);
}else{
draw_line($x1, $y1, $x2, $y2);
}
}
for($i = 0; $i <= 4; ++$i){
$y = -14.8 + $i * 2.6;
fractale(0, $y, 15, $y, $i);
}
allocate_text_color('blue');
draw_text('Fractale', $x = 7.5, $y = -14, $o_pos = O_POS_LOW_CENTER);
unit_vector(&$u, &$v); //ベクトルを長さ1の単位ベクトルにする。もとのベクトルの長さを関数値でもどす。 //$u ベクトルの x 座標 //$v ベクトルの y 座標 $ang = calc_angle($u, $v); //ベクトルの角度(ラジアン)を関数値でもどす。 //$u ベクトルの x 座標 //$v ベクトルの y 座標 $ang = normalize_ang($ang); //ラジアン角度を 0から 2pi までに正規化して関数値でもどす。 //$ang ラジアン角度 $da = calc_da($ea, $sa); //開始角度からみた終了角度の増分角を正規化して関数値で返す(0から 2piに正規化) //$ea ラジアン開始角度 //$sa ラジアン終了角度 $prod = calc_intersec_pt_of_lines($s1x, $s1y, $v1x, $v1y, $s2x, $s2y, $v2x, $v2y, &$k, &$l, &$px, &$py); //ニ直線の交点を求める // (関数値で、直線1の始点から終点へ向かうベクトルと直線2の始点から終点へ向かうベクトルの外積を返す) // (関数値が 0 ならば、平行線のため 求まらず) //$s1x, $s1y 直線1の始点 //$v1x, $v1y 直線1の始点から終点へ向かうベクトル //$s2x, $s2y 直線2の始点 //$v2x, $v2y 直線2の始点から終点へ向かうベクトル //$k, 交点の直線1のベクトルに掛ける係数 //$l, 交点の直線2のベクトルに掛ける係数 //$px, $py 交点(戻される) calc_intersec_pt_of_lns($s1x, $s1y, $e1x, $e1y, $s2x, $s2y, $e2x, $e2y, &$px, &$py); //ニ直線の交点を求める // (関数値で、直線1の始点から終点へ向かうベクトルと直線2の始点から終点へ向かうベクトルの外積を返す) // (関数値が 0 ならば、平行線のため 求まらず) //$s1x, $s1y 直線1の始点 //$e1x, $e1y 直線1の終点 //$s2x, $s2y 直線2の始点 //$e2x, $e2y 直線2の終点 //$px, $py 交点(戻される) rot90_vec($vx, $vy, &$ux90, &$uy90); //ベクトルを90度回転する //$vx, $vy ベクトル //$ux90, $uy90 90度回転したベクトル rot_vec($cos_ang, $sin_ang, $vx, $vy, &$rot_x, &$rot_y); //ベクトルを回転する //$cos_ang, $sin_ang 回転角の cos sin //$vx, $vy ベクトル //$rot_x, $rot_y 回転したベクトル calc_perpendicular_bisector($s1x, $s1y, $e1x, $e1y, &$mx, &$my, &$vx, &$vy); //直線1の垂直二等分線を求める //$s1x, $s1y 直線1の始点 //$e1x, $e1y 直線1の終点 //$mx, $my 直線1の中点(=垂直二等分線の始点) //$vx, $vy 垂直二等分線の始点から終点へ向かうベクトル $dist = calc_distance($ax, $ay, $bx, $by); //二点の距離を求める //$ax, $ay 点1 //$bx, $by 点2 $prod = calc_circumscribed_circle($ax, $ay, $bx, $by, $cx, $cy, &$cent_x, &$cent_y, &$r); //三角形の外接円を求める // (関数値で外積を返す、 0の場合、三角形が異常な形で、求まらず) //$ax, $ay, $bx, $by, $cx, $cy 三角形の頂点 //$cent_x, $cent_y 外接円の中心点 //$r 外接円の半径 $dist = calc_didtance_to_line($px, $py, $ax, $ay, $vx, $vy); //点から直線までの距離を求め、関数値で返す //$px, $py 点 //$ax, $ay 直線1の始点 //$vx, $vy 直線1の始点から終点へ向かうベクトル $prod = calc_foot_of_perpendicular_line(&$fx, &$fy, $px, $py, $ax, $ay, $vx, $vy); //点から直線へ下ろした垂線の足を求める // (関数値で外積を返す、 0の場合、異常な形で、求まらず) //$fx, $fy 垂線の足 //$px, $py 点 //$ax, $ay 直線1の始点 //$vx, $vy 直線1の始点から終点へ向かうベクトル calc_parallel_line(&$s2x, &$s2y, &$e2x, &$e2y, $dist, $s1x, $s1y, $e1x, $e1y) //直線1(線分)の平行線を求める // (関数値はなし) // $s2x, $s2y, $e2x, $e2y 求める直線2の始点と終点 // $dist 平行線の間隔(正の数なら始点から終点に向かって左側に平行線を求める、負の数なら右側に求める) // $s1x, $s1y, $e1x, $e1y 基準となる直線1の始点と終点 $l = calc_foot_of_perpendicular_circle(&$fx_near, &$fy_near, &$fx_far, &$fy_far, $px, $py, $cx, $cy, $r); //点から円へ下ろした垂線の足を求める // (関数値で中心点から点1までの距離を返す、 0の場合、異常な形で、求まらず) //$fx_near, $fy_near 垂線の足(近いほう) //$fx_far, $fy_far 垂線の足(遠いほう) //$px, $py 点1 //$cx, $cy 円中心点 //$r 円の半径 $dist = calc_intersec_pts_of_line_circle(&$ix_fore, &$iy_fore, &$ix_back, &$iy_back, $ax, $ay, $vx, $vy, $cx, $cy, $r); //直線と円の交点を求める // (関数値で中心点から直線までの距離を返す、 $rより大きいの場合、異常な形で、求まらず) //$ix_fore, $iy_fore 交点 直線1の始点に近い方 //$ix_back, $iy_back 交点 直線1の始点から遠い方 //$ax, $ay 直線1の始点 //$vx, $vy 直線1の始点から終点へ向かうベクトル //$cx, $cy 円中心点 //$r 円の半径 $dist = calc_intersec_pts_of_circles(&$ix_right, &$iy_right, &$ix_left, &$iy_left, $c1x, $c1y, $r1, $c2x, $c2y, $r2); //円1と円2の交点を求める // (関数値で中心点と中心点の距離を返す、 // 半径の和より大きいの場合、異常な形で、求まらず) // 半径の差より小さいの場合、異常な形で、求まらず) // 0の場合、異常な形で、求まらず) //$ix_right, $iy_right 円1の中心点から円2の中心点へ向かって右の交点 //$ix_left, $iy_left 円1の中心点から円2の中心点へ向かって左の交点 //$c1x, $c1y, $r1 円1 //$c2x, $c2y, $r2 円2 $prod = calc_inscribed_circle($ax, $ay, $bx, $by, $cx, $cy, &$cent_x, &$cent_y, &$r, &$px, &$py, &$qx, &$qy, &$rx, &$ry); //三角形の内接円を求める // (関数値で外積を返す、 0の場合、三角形が異常な形で、求まらず) //$ax, $ay, $bx, $by, $cx, $cy 三角形の頂点 //$cent_x, $cent_y 内接円の中心点 //$r 内接円の半径 //$px, $py 辺a (辺BC)上の接点 //$qx, $qy 辺b (辺CA)上の接点 //$rx, $ry 辺c (辺AB)上の接点 $r = calc_2p_arc($ax, $ay, $bx, $by, $width, &$cent_x, &$cent_y, &$r, &$sa, &$ea); //二点を通り、弧のふくらみが指定の円弧を求める //$ax, $ay 始点 //$bx, $by 終点 // (円弧の中心は、始点かせ終点に向かって、左にある。) //$width 弦のふくらみ //$cent_x, $cent_y 円の中心点 //$r 円の半径 //$sa 円弧の始点の角 //$ea 円弧の終点の角 calc_3dview(&$x, &$y, $scale2, $rot2, $m2x, $m2y, $x3, $y3, $z3, $f_x, $f_y, $f_z, $view_r, $ang_theta, $ang_varphi); //三次元の座標点を透視変換してニ次元の座標にします。 //$x, $y 変換されたニ次元の座標 //$scale2, $rot2, $m2x, $m2y 透視変換の直後に行う、ニ次元上の倍率・回転・平行移動 //$x3, $y3, $z3 変換したい三次元の座標点 //$f_x, $f_y, $f_z 三次元の注視点(物体の中心) //$view_r 注視点から視点(目の位置)までの距離 //$ang_theta 注視点から視点(目の位置)の方向へのXY平面での回転角度(ラジアン) //$ang_varphi 注視点から視点(目の位置)の方向へのXY平面からZ方向への立ち上がり回転角度(ラジアン)
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
function pythagoras($cent_x, $cent_y, $len_c = 4, $ang_a = 1, $mode = 0)
{
$len_b = $len_c * cos($ang_a);
$len_a = $len_c * sin($ang_a);
$ax = $cent_x;
$ay = $cent_y;
$bx = $ax + $len_c ;
$by = $ay;
$cx = $ax + $len_b * cos($ang_a);
$cy = $ay + $len_b * sin($ang_a);
$a1x = $ax;
$a1y = $ay - $len_c;
$a2x = $ax + $len_b * cos($ang_a + M_PI / 2);
$a2y = $ay + $len_b * sin($ang_a + M_PI / 2);
$a3x = $ax;
$a3y = $ay + $len_c;
$b1x = $bx;
$b1y = $by - $len_c;
$b2x = $bx + $len_a * cos($ang_a);
$b2y = $by + $len_a * sin($ang_a);
$b3x = $bx;
$b3y = $by + $len_c;
$c1x = $cx + $len_b * cos($ang_a + M_PI / 2);
$c1y = $cy + $len_b * sin($ang_a + M_PI / 2);
$c2x = $cx + $len_a * cos($ang_a);
$c2y = $cy + $len_a * sin($ang_a);
$c3x = $cx;
$c3y = $ay;
$c4x = $cx;
$c4y = $a1y;
$c5x = $c1x + $len_a * cos($ang_a);
$c5y = $c1y + $len_a * sin($ang_a);
/*
allocate_color('purple');
allocate_bgcolor('yellow');
draw_line($ax, $ay, $bx, $by);
draw_line($bx, $by, $cx, $cy);
draw_line($cx, $cy, $ax, $ay);
draw_line($c3x, $c3y, $c4x, $c4y);
*/
if($mode == 0 || $mode == 1){
allocate_color('#FFD700');
fill_quadrangle($ax, $ay, $cx, $cy, $c1x, $c1y, $a2x, $a2y);
}else if($mode == 2 || $mode == 3){
allocate_color('#FFD700');
fill_quadrangle($ax, $ay, $cx, $cy, $c5x, $c5y, $a3x, $a3y);
}
if($mode == 0 || $mode == 1){
allocate_color('#87CEEB');
fill_quadrangle($cx, $cy, $bx, $by, $b2x, $b2y, $c2x, $c2y);
}else if($mode == 2 || $mode == 3){
allocate_color('#87CEEB');
fill_quadrangle($cx, $cy, $bx, $by, $b3x, $b3y, $c5x, $c5y);
}
if($mode == 0 || $mode == 1 || $mode == 2){
allocate_color('#FF69B4');
fill_quadrangle($ax, $ay, $bx, $by, $b1x, $b1y, $a1x, $a1y);
}else{
allocate_color('#FFD700');
fill_quadrangle($ax, $ay, $c3x, $c3y, $c4x, $c4y, $a1x, $a1y);
allocate_color('#87CEEB');
fill_quadrangle($c3x, $c3y, $c4x, $c4y, $b1x, $b1y, $bx, $by);
}
allocate_color('black');
draw_line($ax, $ay, $a1x, $a1y);
draw_line($ax, $ay, $a2x, $a2y);
draw_line($a1x, $a1y, $b1x, $b1y);
draw_line($bx, $by, $b1x, $b1y);
draw_line($bx, $by, $b2x, $b2y);
draw_line($b2x, $b2y, $c2x, $c2y);
draw_line($cx, $cy, $c1x, $c1y);
draw_line($cx, $cy, $c2x, $c2y);
draw_line($c1x, $c1y, $a2x, $a2y);
allocate_color('black');
draw_marked_triangle($ax, $ay, $bx, $by, $cx, $cy,
$type_a = 0, $type_b = 0, $type_c = 1,
$text_a = '', $text_b = '', $text_c = '',
$text_ops_a = 'A', $text_ops_b = 'B', $text_ops_c = 'C',
$italic = true, $italic_ops = false, $r = 10);
if($mode == 0){
draw_text('a', ($bx + $cx) / 2, ($by + $cy) / 2, O_POS_LOW_LEFT);
draw_text('b', ($cx + $ax) / 2, ($cy + $ay) / 2, O_POS_LOW_RIGHT);
draw_text('c', ($ax + $bx) / 2, ($ay + $by) / 2 - $len_c / 10, O_POS_UP_CENTER);
}
if($mode == 1){
allocate_color('red');
draw_line($cx, $cy, $c5x, $c5y);
draw_line($c2x, $c2y, $c5x, $c5y);
draw_line($c1x, $c1y, $c5x, $c5y);
}else if($mode == 2){
allocate_color('red');
set_thick($thick = 3);
draw_line($cx, $cy, $c5x, $c5y);
draw_line($b3x, $b3y, $c5x, $c5y);
draw_line($b3x, $b3y, $bx, $by);
draw_line($bx, $by, $cx, $cy);
draw_line($a3x, $a3y, $c5x, $c5y);
draw_line($a3x, $a3y, $ax, $ay);
draw_line($cx, $cy, $ax, $ay);
set_thick($thick = 1);
}else if($mode == 3){
allocate_color('red');
set_thick($thick = 1);
draw_line($c3x, $c3y, $c5x, $c5y);
draw_line($b3x, $b3y, $c5x, $c5y);
draw_line($b3x, $b3y, $bx, $by);
draw_line($bx, $by, $cx, $cy);
draw_line($a3x, $a3y, $c5x, $c5y);
draw_line($a3x, $a3y, $ax, $ay);
draw_line($cx, $cy, $ax, $ay);
set_thick($thick = 3);
draw_line($c3x, $c3y, $c4x, $c4y);
draw_line($ax, $ay, $bx, $by);
draw_line($bx, $by, $b1x, $b1y);
draw_line($b1x, $b1y, $a1x, $a1y);
draw_line($a1x, $a1y, $ax, $ay);
set_thick($thick = 1);
}
}
pythagoras($x = -12, $y = 6.3, $len = 6, $ang = M_PI / 3, $mode = 0);
pythagoras($x = 3, $y = 6.3, $len = 6, $ang = M_PI / 3, $mode = 1);
pythagoras($x = -12, $y = -8.8, $len = 6, $ang = M_PI / 3, $mode = 2);
pythagoras($x = 3, $y = -8.8, $len = 6, $ang = M_PI / 3, $mode = 3);
set_text_size(8);
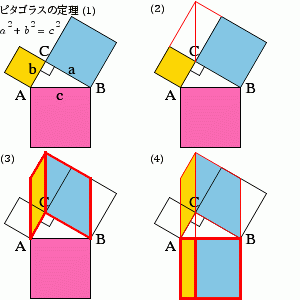
draw_text('ピタゴラスの定理 (1)', -15, 15, O_POS_UP_LEFT, 'ipamp');
draw_formula('a^2+b^2=c^2', $size = 9, -15, 13, O_POS_UP_LEFT);
draw_text('(2)', 0, 15, O_POS_UP_LEFT, 'ipamp');
draw_text('(3)', -15, 0, O_POS_UP_LEFT, 'ipamp');
draw_text('(4)', 0, 0, O_POS_UP_LEFT, 'ipamp');
set_scale($scale = 10, $org_x_percent = 50, $org_y_percent = 50);
function f_out($ax, $ay, $bx, $by, $cx, $cy)
{
calc_circumscribed_circle($ax, $ay, $bx, $by, $cx, $cy, $cent_x, $cent_y, $r);
allocate_color('black');
draw_marked_triangle($ax, $ay, $bx, $by, $cx, $cy,
$type_a = 1, $type_b = 0, $type_c = 0,
$text_a = '', $text_b = '', $text_c = '',
$text_ops_a = 'A', $text_ops_b = 'B', $text_ops_c = 'C',
$italic = true, $italic_ops = false, 10);
allocate_color('red');
draw_circle($cent_x, $cent_y, $r);
allocate_color('black');
$dx = $bx + 2 * ($cent_x - $bx);
$dy = $by + 2 * ($cent_y - $by);
draw_marked_triangle($dx, $dy, $bx, $by, $cx, $cy,
$type_a = 1, $type_b = 0, $type_c = 3,
$text_a = '', $text_b = '', $text_c = '',
$text_ops_a = 'D', $text_ops_b = '', $text_ops_c = '',
$italic = true, $italic_ops = false, $r = 10);
draw_text('o', $cent_x, $cent_y, O_POS_UP_LEFT);
draw_arc_mark($tx, $ty, $dx, $dy, $bx, $by, $text = '2R', $italic = true,
$arc_type = ARC_TYPE_DASH, $width_rate = 1, $text_hole_rate = 3);
draw_arc_mark($tx, $ty, $bx, $by, $cx, $cy, $text = 'a', $italic = true,
$arc_type = ARC_TYPE_NONE, $width_rate = 1, $text_hole_rate = 3);
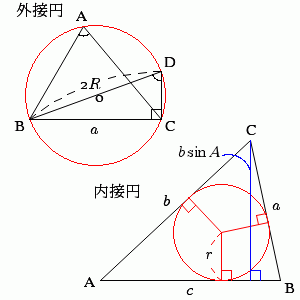
draw_text('外接円', $ax - 2, $ay + 1, O_POS_LOW_RIGHT);
}
$ox = -5.5;
$oy = 5.5;
$r = 7;
$ax = $ox + $r * cos(deg2rad(100));
$ay = $oy + $r * sin(deg2rad(100));
$bx = $ox + $r * cos(deg2rad(200));
$by = $oy + $r * sin(deg2rad(200));
$cx = $ox + $r * cos(deg2rad(340));
$cy = $oy + $r * sin(deg2rad(340));
f_out($ax, $ay, $bx, $by, $cx, $cy);
function f_in($ax, $ay, $bx, $by, $cx, $cy)
{
calc_inscribed_circle($ax, $ay, $bx, $by, $cx, $cy, $cent_x, $cent_y, $r,
$px, $py, $qx, $qy, $rx, $ry);
allocate_color('black');
draw_marked_triangle($ax, $ay, $bx, $by, $cx, $cy,
$type_a = 0, $type_b = 0, $type_c = 0,
$text_a = '', $text_b = '', $text_c = '',
$text_ops_a = 'A', $text_ops_b = 'B', $text_ops_c = 'C',
$italic = true, $italic_ops = false, 10);
draw_arc_mark($tx, $ty, $bx, $by, $cx, $cy, $text = 'a', $italic = true,
$arc_type = ARC_TYPE_NONE, $width_rate = 1, $text_hole_rate = 3);
draw_arc_mark($tx, $ty, $cx, $cy, $ax, $ay, $text = 'b', $italic = true,
$arc_type = ARC_TYPE_NONE, $width_rate = 1, $text_hole_rate = 3);
draw_arc_mark($tx, $ty, $ax, $ay, $bx, $by, $text = 'c', $italic = true,
$arc_type = ARC_TYPE_NONE, $width_rate = 1, $text_hole_rate = 3);
allocate_color('red');
draw_circle($cent_x, $cent_y, $r);
draw_line($cent_x, $cent_y, $px, $py);
draw_line($cent_x, $cent_y, $qx, $qy);
draw_line($cent_x, $cent_y, $rx, $ry);
draw_corner_mark($px, $py, $cx, $cy, $cent_x, $cent_y, $type = 1,
$text = '', $italic = true, $text_ops = '', $italic_ops = false, 10);
draw_corner_mark($qx, $qy, $ax, $ay, $cent_x, $cent_y, $type = 1,
$text = '', $italic = true, $text_ops = '', $italic_ops = false, 10);
draw_corner_mark($rx, $ry, $bx, $by, $cent_x, $cent_y, $type = 1,
$text = '', $italic = true, $text_ops = '', $italic_ops = false, 10);
draw_arc_mark($tx, $ty, $cent_x, $cent_y, $rx, $ry, $text = 'r', $italic = true,
$arc_type = ARC_TYPE_DASH, $width_rate = 1, $text_hole_rate = 2);
allocate_color('blue');
calc_foot_of_perpendicular_line($fx, $fy, $cx, $cy, $ax, $ay, $bx - $ax, $by - $ay);
draw_line($cx, $cy, $fx, $fy);
draw_corner_mark($fx, $fy, $bx, $by, $cx, $cy, $type = 1,
$text = '', $italic = true, $text_ops = '', $italic_ops = false, 10);
$kx = ($cx * 4 + $fx) / 5;
$ky = ($cy * 4 + $fy) / 5;
$lx = ($cx * 9 + $fx) / 10;
$ly = ($cy * 9 + $fy) / 10;
$ux = $lx - $kx;
$uy = $ly - $ky;
rot90_vec($ux, $uy, $vx, $vy);
$tx = $lx + 2 * $vx;
$ty = $ly + 2 * $vy;
calc_2p_arc($kx, $ky, $tx, $ty, $r / 8, $cx1, $cy1, $r1, $sa1, $ea1);
draw_arc($cx1, $cy1, $r1, $sa1, $ea1);
draw_formula($formula_text = 'b sin A', $size = 12, $tx, $ty, $o_pos = O_POS_MIDDLE_RIGHT);
draw_text('内接円', $qx - 5, $qy, O_POS_LOW_RIGHT);
}
f_in($ax = -5, $ay = -13, $bx = 13, $by = -13, $cx = 10, $cy = 1);
clear_canvas(); //画像全体を背景色で塗ります。 set_alphablending($alpha = 50); //塗りつぶしのときの、透明度を指定します。 // (透明度は、0 から 127 までの値。 0 は完全に不透明な状態。 127 は完全に透明な状態を表します。) set_antialias($antialias = true); //直線や多角形を高速に描画するためのアンチエイリアス機能を有効/無効にします。 //$antialias true false transparent_gif_bgcolor(); //背景色を透明にします。 // (gif 画像形式のときのみ有効となります。) // WEBブラウザ上、この背景色は透明になり、背景が透けて見えます。
xf($x); //作図のx座標から画像内部のx座標に変換し、関数値で返します。 x_rev($x); //画像内部のx座標から作図のx座標に変換し、関数値で返します。 yf($y); //作図のy座標から画像内部のy座標に変換し、関数値で返します。 y_rev($y); //画像内部のy座標から作図のy座標に変換し、関数値で返します。